Anàlisi detallada del circuit de la sèrie RC
2024-05-08
20601
El circuit de la sèrie RC, que consisteix en una resistència i un condensador, serveix de component fonamental tant en dissenys bàsics com en els sistemes electrònics bàsics.Ajuda a comprendre principis clau com la resposta de freqüència, el canvi de fase i el filtratge de senyal, que tenen un paper significatiu en el disseny del circuit i el processament del senyal.Aquesta exploració abasta els conceptes bàsics teòrics i s’estén a aplicacions pràctiques mitjançant experiments i simulacions.Muntant físicament el circuit o modelant -lo digitalment, els estudiants poden comprendre visualment el procés de càrrega i els efectes dels ions components V ariat, fent que els conceptes complexos siguin més accessibles i memorables.
Catàleg

Figura 1: diferents tensions de sortida dels circuits RC
Introducció al circuit RC
Un circuit RC, curt per al circuit de resistència a la resistència, és fonamental en l'electrònica per a la manipulació de senyals a través de resistències i condensadors.Aquests circuits són especialment coneguts per la seva capacitat de canviar les fases i els senyals de filtre, utilitzant arranjaments senzills d’aquests components.Un circuit bàsic RC, sovint conegut com a circuit RC de primer ordre, normalment inclou una sola resistència i un condensador.
En una configuració típica, la tensió d’entrada s’aplica a la disposició de la sèrie d’una resistència i un condensador.La sortida es pot dibuixar a través de la resistència o del condensador, cadascuna donant respostes diferents a les freqüències de senyal a causa de les característiques úniques del condensador.Aquesta versatilitat permet als circuits RC realitzar una varietat de rols en dispositius electrònics, com ara senyals d’acoblament i filtratge o fins i tot convertir les formes d’ona quan se sotmeten a un voltatge de pas.
El circuit RC es pot configurar de diverses maneres: a la sèrie, paral·lel o una combinació d’ambdós, coneguts com a sèries-paral·leles.Cada configuració afecta de manera diferent les freqüències del senyal: les connexions de sèries tendeixen a atenuar freqüències baixes, mentre que les connexions paral·leles s’utilitzen per amortir freqüències més altes.Aquesta diferència es deu principalment a la manera en què les resistències i els condensadors interaccionen amb el circuit;Les resistències s’oposen directament al corrent mentre els condensadors l’emmagatzemen i l’alliberen, afectant com el circuit respon a diferents freqüències.
A diferència dels circuits que inclouen inductors, com els circuits LC, els circuits RC simples no poden ressonar, ja que les resistències no emmagatzemen energia.Aquest atribut influeix de manera clara com s’utilitzen els circuits RC, centrats en la seva capacitat de filtració en lloc d’emmagatzematge o ressonància d’energia.Cada configuració serveix per a un propòsit específic, fent que els circuits RC siguin eines versàtils tant en l'estudi teòric com en l'aplicació pràctica en el disseny electrònic.
Circuit de la sèrie RC
Un circuit de la sèrie RC, essencialment compost per una resistència (R) i un condensador (C) en sèrie, opera amb un principi senzill.Quan l’interruptor del circuit està tancat, el condensador comença a carregar -se des de la tensió aplicada (V), iniciant un flux de corrent a través del circuit.A mesura que el condensador es carrega, el corrent augmenta gradualment fins que el condensador arriba a la seva capacitat, en aquest moment deixa d’acceptar la càrrega i el corrent s’estabilitza al seu valor màxim, calculat com a 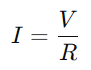 .
.
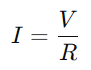 .
.El procés de càrrega del condensador es pot descriure matemàticament per l'equació 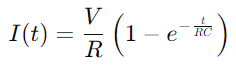 , on sóc el corrent, V és la tensió, R és la resistència, C és la capacitança, T és el moment i E és la base del logaritme natural.Aquesta fórmula reflecteix com el corrent canvia amb el pas del temps a mesura que el condensador es carrega, amb el producte dels valors de resistència i capacitança (RC) que defineixen la constant de temps del circuit, indicatiu de la velocitat a la qual es carrega el condensador.
, on sóc el corrent, V és la tensió, R és la resistència, C és la capacitança, T és el moment i E és la base del logaritme natural.Aquesta fórmula reflecteix com el corrent canvia amb el pas del temps a mesura que el condensador es carrega, amb el producte dels valors de resistència i capacitança (RC) que defineixen la constant de temps del circuit, indicatiu de la velocitat a la qual es carrega el condensador.
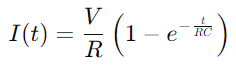 , on sóc el corrent, V és la tensió, R és la resistència, C és la capacitança, T és el moment i E és la base del logaritme natural.Aquesta fórmula reflecteix com el corrent canvia amb el pas del temps a mesura que el condensador es carrega, amb el producte dels valors de resistència i capacitança (RC) que defineixen la constant de temps del circuit, indicatiu de la velocitat a la qual es carrega el condensador.
, on sóc el corrent, V és la tensió, R és la resistència, C és la capacitança, T és el moment i E és la base del logaritme natural.Aquesta fórmula reflecteix com el corrent canvia amb el pas del temps a mesura que el condensador es carrega, amb el producte dels valors de resistència i capacitança (RC) que defineixen la constant de temps del circuit, indicatiu de la velocitat a la qual es carrega el condensador.
Figura 2: Circuit de la sèrie RC
La descàrrega es produeix quan s’obre l’interruptor, invertint el procés: l’energia emmagatzemada al condensador s’allibera, fent que el corrent flueixi en sentit contrari fins que el condensador es dreni.Aquest cicle de càrrega i descàrrega és crucial en aplicacions com ara els circuits de conversió, filtratge i sincronització de senyal a causa de la manera previsible de canviar el corrent i la tensió.

Figura 3: curtcircuit de la sèrie RC
El comportament del circuit de la sèrie RC també varia amb la freqüència.A baixes freqüències, el condensador actua més com un circuit obert, impedint molt el flux de corrent.A mesura que la freqüència augmenta, la reactància capacitiva disminueix, facilitant el pas del corrent.Aquest canvi d’impedància amb freqüència permet al circuit de la sèrie RC actuar com a filtre, atenuant selectivament les freqüències per sota d’un determinat llindar (freqüència de gir 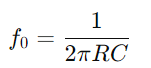 )).
)).
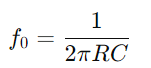 )).
)).
Figura 4: Càrrega i descàrrega dels circuits de la sèrie RC
A més de les operacions en estat estacionari, també s’estudien els circuits RC per a les seves respostes transitòries quan se sotmeten a canvis sobtats de tensió, com per exemple quan s’encén o s’apaga una font d’alimentació de corrent continu.Aquest escenari s’anomena procés transitori, on el circuit es transmet d’un estat estable a un altre.La dinàmica d’aquest procés depèn significativament de la constant de temps RC, que regeix la rapidesa amb què reacciona el circuit als canvis.
En última instància, els circuits de la sèrie RC serveixen múltiples funcions tant en aplicacions de corrent continu com de CA, manejant tasques que van des de retardar els senyals fins a la integració o acoblar diversos elements de circuit.Aquesta versatilitat prové de les interaccions úniques entre la resistència i el condensador, que determinen junts la resposta global del circuit a canvis de tensió i freqüència.

Figura 5: Diagrama de circuits de la sèrie RC i fórmula de freqüència
En un circuit de la sèrie RC, la interacció entre la resistència (R) i el condensador (C) influeix tant en el flux de corrent com en la distribució de tensió.El paper principal de la resistència és regular el flux actual.Aquesta relació es quantifica per la llei d'Ohm, que afirma 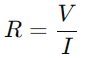 , on V és tensió i Jo és actual.Essencialment, la resistència actua com un coll d’ampolla, controlant la quantitat d’electricitat que pot passar en un moment donat.
, on V és tensió i Jo és actual.Essencialment, la resistència actua com un coll d’ampolla, controlant la quantitat d’electricitat que pot passar en un moment donat.
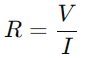 , on V és tensió i Jo és actual.Essencialment, la resistència actua com un coll d’ampolla, controlant la quantitat d’electricitat que pot passar en un moment donat.
, on V és tensió i Jo és actual.Essencialment, la resistència actua com un coll d’ampolla, controlant la quantitat d’electricitat que pot passar en un moment donat.La funció del condensador és lleugerament més complexa, ja que emmagatzema temporalment l’energia elèctrica i després la torna a alliberar al circuit.La tensió a través del condensador (VC) es correlacionen amb la seva càrrega emmagatzemada (P) i es calcula mitjançant la fórmula 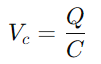 .Aquesta relació posa de manifest la capacitat del condensador per mantenir la càrrega, afectant directament la tensió que presenta.Durant el funcionament, la dinàmica de la càrrega i la descàrrega del condensador són vitals per comprendre els circuits RC.La constant de temps (τ), definit com
.Aquesta relació posa de manifest la capacitat del condensador per mantenir la càrrega, afectant directament la tensió que presenta.Durant el funcionament, la dinàmica de la càrrega i la descàrrega del condensador són vitals per comprendre els circuits RC.La constant de temps (τ), definit com 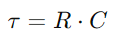 , mesura la rapidesa amb què el condensador arriba aproximadament al 63,2% de la tensió completa subministrada per la font (V0)).Aquesta constant de temps és indicativa de com el circuit s’adapta als canvis d’entrada, amb les propietats de resistència i condensador que dicten el ritme d’aquests ajustaments.
, mesura la rapidesa amb què el condensador arriba aproximadament al 63,2% de la tensió completa subministrada per la font (V0)).Aquesta constant de temps és indicativa de com el circuit s’adapta als canvis d’entrada, amb les propietats de resistència i condensador que dicten el ritme d’aquests ajustaments.
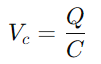 .Aquesta relació posa de manifest la capacitat del condensador per mantenir la càrrega, afectant directament la tensió que presenta.Durant el funcionament, la dinàmica de la càrrega i la descàrrega del condensador són vitals per comprendre els circuits RC.La constant de temps (τ), definit com
.Aquesta relació posa de manifest la capacitat del condensador per mantenir la càrrega, afectant directament la tensió que presenta.Durant el funcionament, la dinàmica de la càrrega i la descàrrega del condensador són vitals per comprendre els circuits RC.La constant de temps (τ), definit com 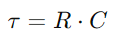 , mesura la rapidesa amb què el condensador arriba aproximadament al 63,2% de la tensió completa subministrada per la font (V0)).Aquesta constant de temps és indicativa de com el circuit s’adapta als canvis d’entrada, amb les propietats de resistència i condensador que dicten el ritme d’aquests ajustaments.
, mesura la rapidesa amb què el condensador arriba aproximadament al 63,2% de la tensió completa subministrada per la font (V0)).Aquesta constant de temps és indicativa de com el circuit s’adapta als canvis d’entrada, amb les propietats de resistència i condensador que dicten el ritme d’aquests ajustaments.La tensió a través del condensador en un moment donat durant la càrrega es dóna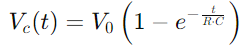 , il·lustrant un augment no lineal a mesura que el condensador s’omple.Aquesta equació descriu com la taxa de càrrega s’alenteix a mesura que el condensador s’acosta a la capacitat completa.
, il·lustrant un augment no lineal a mesura que el condensador s’omple.Aquesta equació descriu com la taxa de càrrega s’alenteix a mesura que el condensador s’acosta a la capacitat completa.
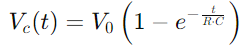 , il·lustrant un augment no lineal a mesura que el condensador s’omple.Aquesta equació descriu com la taxa de càrrega s’alenteix a mesura que el condensador s’acosta a la capacitat completa.
, il·lustrant un augment no lineal a mesura que el condensador s’omple.Aquesta equació descriu com la taxa de càrrega s’alenteix a mesura que el condensador s’acosta a la capacitat completa.Per contra, durant la descàrrega, la tensió del condensador disminueix segons 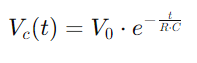 , retratant una disminució lineal de l’energia emmagatzemada amb el pas del temps.Aquest procés proporciona una imatge clara de com l’energia s’allibera del condensador de nou al circuit.En aplicacions de CA, la diferència de fase entre la tensió i el corrent, φ, esdevé crític.Aquesta diferència, calculada com
, retratant una disminució lineal de l’energia emmagatzemada amb el pas del temps.Aquest procés proporciona una imatge clara de com l’energia s’allibera del condensador de nou al circuit.En aplicacions de CA, la diferència de fase entre la tensió i el corrent, φ, esdevé crític.Aquesta diferència, calculada com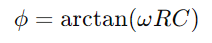 on ω Representa la freqüència angular, mostra el retard causat pel condensador, que afecta la sincronització entre quan els fluxos de corrent i la tensió canvia entre els components.
on ω Representa la freqüència angular, mostra el retard causat pel condensador, que afecta la sincronització entre quan els fluxos de corrent i la tensió canvia entre els components.
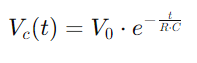 , retratant una disminució lineal de l’energia emmagatzemada amb el pas del temps.Aquest procés proporciona una imatge clara de com l’energia s’allibera del condensador de nou al circuit.En aplicacions de CA, la diferència de fase entre la tensió i el corrent, φ, esdevé crític.Aquesta diferència, calculada com
, retratant una disminució lineal de l’energia emmagatzemada amb el pas del temps.Aquest procés proporciona una imatge clara de com l’energia s’allibera del condensador de nou al circuit.En aplicacions de CA, la diferència de fase entre la tensió i el corrent, φ, esdevé crític.Aquesta diferència, calculada com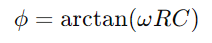 on ω Representa la freqüència angular, mostra el retard causat pel condensador, que afecta la sincronització entre quan els fluxos de corrent i la tensió canvia entre els components.
on ω Representa la freqüència angular, mostra el retard causat pel condensador, que afecta la sincronització entre quan els fluxos de corrent i la tensió canvia entre els components.En general, la resistència limita i dirigeix el flux de corrent mentre el condensador emmagatzema i modula la tensió.En conjunt, determinen les característiques de resposta del circuit, com ara la rapidesa amb què es pot carregar i descàrrega i els canvis de fase que es produeixen en els escenaris de corrent altern.Aquest comportament combinat fonamenta les operacions fonamentals dels circuits de la sèrie RC, fent -los integrals en diverses aplicacions electròniques.
Equacions bàsiques del circuit de la sèrie RC
Per entendre el comportament d’un circuit de la sèrie RC, és crucial començar amb les equacions bàsiques que descriuen la seva resposta als canvis en la tensió d’entrada.Suposem que tenim una tensió d’entrada canviant representada com a Vin (t), amb la tensió a través de la resistència etiquetada com a Vr (t) i a través del condensador com VC (T).En un circuit de sèrie, el mateix corrent, I (t) flueix a través de la resistència i el condensador.
L’aplicació de la llei de tensió de Kirchhoff (KVL), que afirma que la tensió total al voltant de qualsevol bucle tancat en un circuit ha d’igualtar zero, trobem que la tensió d’entrada és igual a la suma de les tensions a través de la resistència i el condensador:

La tensió a través de la resistència es pot calcular mitjançant la llei d'Ohm:
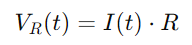
Per al condensador, la tensió VC (t) està relacionada amb la càrrega q (t) que es manté, donada per:
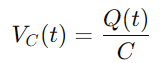
Com que el corrent es defineix com la taxa de flux de càrrega, tenim:
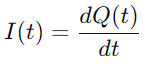
Substituint Q (t) En l'equació per a VC (T), i utilitzant el derivat de càrrega I (t), obtenim l'equació diferencial bàsica del circuit de la sèrie RC:

Substituint encara més Q (t) amb la integral de I (t), ho aconseguim:
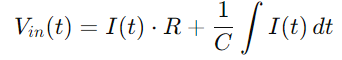
Per al corrent I (t), tenint en compte la velocitat de canvi de tensió a través del condensador, utilitzem:
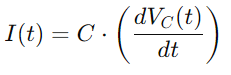
La integració de totes aquestes relacions ens proporciona l’equació diferencial que descriu la tensió a través del condensador:
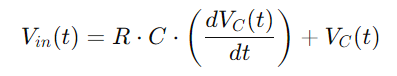
Es tracta d’una equació diferencial lineal de primer ordre que capta el canvi de tensió depenent del temps a través del condensador.La resolució d’aquesta equació ens permet descriure amb precisió com evoluciona la tensió del condensador.Aquesta comprensió és fonamental per analitzar tant els cicles de càrrega i descàrrega del condensador, com la resposta del circuit a diferents freqüències.Aquest enfocament complet proporciona una visió profunda de les característiques dinàmiques del circuit de la sèrie RC.

Figura 6: Equació diferencial de tensió
Impedància del circuit de la sèrie RC
Per reescriure la descripció d’un circuit de la sèrie RC, centrat en la interacció humana i una explicació directa i simplificada, millorem les experiències tangibles i les operacions pas a pas implicades mantenint el missatge bàsic i la coherència:
En un circuit de la sèrie RC, la resistència i el condensador funcionen en conjunt per controlar el flux d’electricitat, crucial quan es tracta de corrents alterns.La impedància total del circuit, representada com a 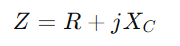 , combina la resistència R i la reactància capacitiva xc.La característica clau d’aquesta configuració és que els valors d’impedància dels dos components varien amb els canvis de freqüència.A mesura que augmenta la freqüència, la impedància del condensador disminueix, permetent passar més corrent, mentre que la resistència es manté essencialment constant.
, combina la resistència R i la reactància capacitiva xc.La característica clau d’aquesta configuració és que els valors d’impedància dels dos components varien amb els canvis de freqüència.A mesura que augmenta la freqüència, la impedància del condensador disminueix, permetent passar més corrent, mentre que la resistència es manté essencialment constant.
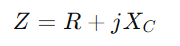 , combina la resistència R i la reactància capacitiva xc.La característica clau d’aquesta configuració és que els valors d’impedància dels dos components varien amb els canvis de freqüència.A mesura que augmenta la freqüència, la impedància del condensador disminueix, permetent passar més corrent, mentre que la resistència es manté essencialment constant.
, combina la resistència R i la reactància capacitiva xc.La característica clau d’aquesta configuració és que els valors d’impedància dels dos components varien amb els canvis de freqüència.A mesura que augmenta la freqüència, la impedància del condensador disminueix, permetent passar més corrent, mentre que la resistència es manté essencialment constant.La impedància, denotada com Z i mesurat en ohms (ω), té un paper crític en la determinació de com reacciona el circuit al corrent altern.Com en els circuits de la sèrie RL, la resistència R i reactància capacitiva xC d’un circuit RC forma un triangle conegut com el triangle d’impedància.Aquest triangle es relaciona estretament amb el triangle de tensió i, aplicant el teorema pitagòric, podeu calcular la impedància total del circuit.

Figura 7: Fórmula de càlcul del circuit de la sèrie RC
Quan es tracta d’aplicacions pràctiques, considereu els auriculars que utilitzin aquests principis.Els auriculars d’alta impedància, que sovint superen els 200 ohms, s’utilitzen normalment amb ordinadors d’escriptori, amplificadors de potència i equips d’àudio professionals.Aquests models d’alta importància coincideixen bé amb les capacitats de sortida de l’electrònica de qualitat professional.Quan s’utilitzen aquests auriculars, és crucial ajustar el volum gradualment per evitar la sobrecàrrega i danyar els delicats components interns, com la bobina de veu.
Per la seva banda, els auriculars de baixa impedància, normalment per sota de 50 ohms, es prefereixen per a dispositius portàtils com ara jugadors de CD, reproductors MD o reproductors de MP3.Aquests auriculars requereixen menys energia per oferir un àudio de gran qualitat, cosa que els fa ideals per a ús mòbil.No obstant això, també necessiten una atenció minuciosa als nivells de sensibilitat per assegurar un rendiment òptim i evitar danys als auriculars o a l’audició.

Figura 8: Diagrama d’impedàncies del circuit de la sèrie RC
Procediments d'admissió i anàlisi dels circuits de la sèrie RC
L’admissió mesura la facilitat que un circuit de la sèrie RC pot conduir electricitat, calculada com la inversa de la impedància (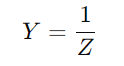 )).Aquest valor integra tant la resistència (R) i la reactància (X) del circuit.La resistència s’oposa al flux actual convertint l’energia elèctrica a la calor, mentre que la reactància emmagatzema l’energia temporalment al circuit.
)).Aquest valor integra tant la resistència (R) i la reactància (X) del circuit.La resistència s’oposa al flux actual convertint l’energia elèctrica a la calor, mentre que la reactància emmagatzema l’energia temporalment al circuit.
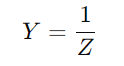 )).Aquest valor integra tant la resistència (R) i la reactància (X) del circuit.La resistència s’oposa al flux actual convertint l’energia elèctrica a la calor, mentre que la reactància emmagatzema l’energia temporalment al circuit.
)).Aquest valor integra tant la resistència (R) i la reactància (X) del circuit.La resistència s’oposa al flux actual convertint l’energia elèctrica a la calor, mentre que la reactància emmagatzema l’energia temporalment al circuit.Per calcular l’admissió
Comença per escriure la impedància 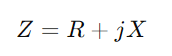 , on R significa resistència, X per a la reactància i j és la unitat imaginària.Utilitzeu la fórmula Y = 1/(R + JX)).Aquesta operació implica números complexos i ens dóna
, on R significa resistència, X per a la reactància i j és la unitat imaginària.Utilitzeu la fórmula Y = 1/(R + JX)).Aquesta operació implica números complexos i ens dóna 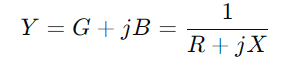 .Aquí, G és la conductança (capacitat de flux de corrent real) i B és la susceptància (la capacitat del circuit de reaccionar davant els canvis en el corrent).
.Aquí, G és la conductança (capacitat de flux de corrent real) i B és la susceptància (la capacitat del circuit de reaccionar davant els canvis en el corrent).
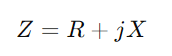 , on R significa resistència, X per a la reactància i j és la unitat imaginària.Utilitzeu la fórmula Y = 1/(R + JX)).Aquesta operació implica números complexos i ens dóna
, on R significa resistència, X per a la reactància i j és la unitat imaginària.Utilitzeu la fórmula Y = 1/(R + JX)).Aquesta operació implica números complexos i ens dóna 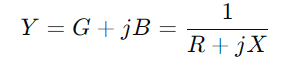 .Aquí, G és la conductança (capacitat de flux de corrent real) i B és la susceptància (la capacitat del circuit de reaccionar davant els canvis en el corrent).
.Aquí, G és la conductança (capacitat de flux de corrent real) i B és la susceptància (la capacitat del circuit de reaccionar davant els canvis en el corrent).
Figura 9: Calculadora de la impedància del circuit de sèries RC
Aquest càlcul revela no només la conductivitat del circuit, sinó també les seves característiques de resposta dinàmiques, crucials per a l’anàlisi del circuit de CA.La conductància i la susceptància, que s’uneixen, indiquen com passa el circuit actual i com emmagatzema i allibera energia.

Figura 10: Fórmula de l'angle de fase
Aplicació pràctica
Els enginyers utilitzen valors d’admissió per millorar el disseny del circuit, especialment en aplicacions d’alta freqüència com ara circuits de freqüència de ràdio.L’ajustament de l’admissió ajuda a la concordança d’impedàncies, reduint la reflexió del senyal i augmentant l’eficiència de la transmissió.
Estudiant la resposta de l’admissió, els enginyers poden avaluar i predir el rendiment del circuit en diverses condicions com la resposta de freqüència, l’estabilitat i la sensibilitat.Equipeu amb un oscil·loscopi i un generador de senyal per mesurar la tensió i el corrent del circuit a freqüències diferents.Centreu -vos especialment en la freqüència de tall per provar les prediccions teòriques i validar -les contra observacions pràctiques.Per als circuits de CA, comenceu per determinar la reactància (xc) del condensador amb 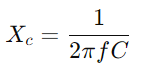 , on f és la freqüència del senyal.Calcula la impedància total
, on f és la freqüència del senyal.Calcula la impedància total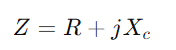 I després l’admissió
I després l’admissió 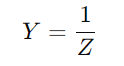 .
.
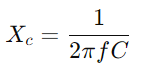 , on f és la freqüència del senyal.Calcula la impedància total
, on f és la freqüència del senyal.Calcula la impedància total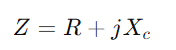 I després l’admissió
I després l’admissió 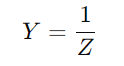 .
.Analitzar la diferència de fase mitjançant 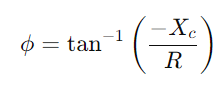 per entendre l’alteració de la forma del senyal.Examineu com el circuit gestiona diferents freqüències, en particular assenyalant el comportament a la freqüència de tall
per entendre l’alteració de la forma del senyal.Examineu com el circuit gestiona diferents freqüències, en particular assenyalant el comportament a la freqüència de tall 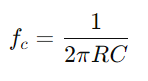 , on el circuit canvia de passar a senyals de bloqueig.L’avaluació de com varien la impedància i la diferència de fase amb la freqüència, és crucial per dissenyar filtres efectius i processadors de senyal.Comenteu com la selectivitat de freqüència, els canvis de fase i l’atenuació del senyal a causa de les propietats del circuit afecten aplicacions pràctiques com el filtratge i l’afinació electrònica.
, on el circuit canvia de passar a senyals de bloqueig.L’avaluació de com varien la impedància i la diferència de fase amb la freqüència, és crucial per dissenyar filtres efectius i processadors de senyal.Comenteu com la selectivitat de freqüència, els canvis de fase i l’atenuació del senyal a causa de les propietats del circuit afecten aplicacions pràctiques com el filtratge i l’afinació electrònica.
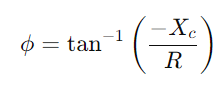 per entendre l’alteració de la forma del senyal.Examineu com el circuit gestiona diferents freqüències, en particular assenyalant el comportament a la freqüència de tall
per entendre l’alteració de la forma del senyal.Examineu com el circuit gestiona diferents freqüències, en particular assenyalant el comportament a la freqüència de tall 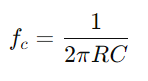 , on el circuit canvia de passar a senyals de bloqueig.L’avaluació de com varien la impedància i la diferència de fase amb la freqüència, és crucial per dissenyar filtres efectius i processadors de senyal.Comenteu com la selectivitat de freqüència, els canvis de fase i l’atenuació del senyal a causa de les propietats del circuit afecten aplicacions pràctiques com el filtratge i l’afinació electrònica.
, on el circuit canvia de passar a senyals de bloqueig.L’avaluació de com varien la impedància i la diferència de fase amb la freqüència, és crucial per dissenyar filtres efectius i processadors de senyal.Comenteu com la selectivitat de freqüència, els canvis de fase i l’atenuació del senyal a causa de les propietats del circuit afecten aplicacions pràctiques com el filtratge i l’afinació electrònica.Aquest enfocament desglossa els processos operatius en passos manejables, enriquint la comprensió de l’usuari amb visions pràctiques sobre la manipulació i l’anàlisi dels circuits de la sèrie RC.

Figura 11: Característiques dels circuits de la sèrie RC
Diagrama de fases del circuit de la sèrie RC
En un circuit de la sèrie RC, tots els elements comparteixen el mateix corrent a causa de la seva configuració de la sèrie.Aquest corrent uniforme actua com a línia de referència del nostre diagrama de fases, que ajuda a visualitzar la relació entre diferents tensions i corrents del circuit.Anem a designar aquest corrent Jo Com a fase de referència, posicionat a zero graus al diagrama.Al diagrama, el corrent Jo s’estableix horitzontalment a la dreta, establint la línia de referència de grau zero.La tensió a través de la resistència (UR) està en fase amb el corrent perquè les resistències no provoquen cap canvi de fase.Per tant, UR es dibuixa com un vector horitzontal en la mateixa direcció que Jo, que s’estén des de l’origen.

Figura 12: Diagrama de fases de circuit de la sèrie RC
En canvi, la tensió a través del condensador (UC) condueix el corrent en 90 graus a causa de la propietat capacitiva de retardar la fase actual.Aquesta tensió està representada per un vector vertical que apunta cap amunt, a partir de la punta del UR vector.La tensió total U Al circuit hi ha la suma vectorial de U Ser UC.Aquesta suma forma un triangle dret amb UR i UC com a costats adjacents i oposats, respectivament.La hipotenusa d’aquest triangle, que s’estén des de l’origen fins a la punta del UC Vector, representa U.
El corrent sinusoïdal a través del circuit és donat pel pecat (ωt), on IM és l'amplitud màxim de corrent i ω és la freqüència angular.En conseqüència, la tensió a través de la resistència és 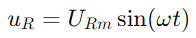 , reflectint la forma d'ona actual.La tensió a través del condensador ve donada per
, reflectint la forma d'ona actual.La tensió a través del condensador ve donada per 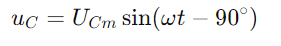 , indicant un canvi de fase de -90 ° (o 90 graus per davant del corrent).El triangle dret del diagrama de fase aclareix això
, indicant un canvi de fase de -90 ° (o 90 graus per davant del corrent).El triangle dret del diagrama de fase aclareix això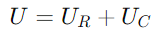 no només està en magnitud, sinó també en relació de fase, amb el vector de tensió del terminal (U) completar el triangle.
no només està en magnitud, sinó també en relació de fase, amb el vector de tensió del terminal (U) completar el triangle.
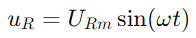 , reflectint la forma d'ona actual.La tensió a través del condensador ve donada per
, reflectint la forma d'ona actual.La tensió a través del condensador ve donada per 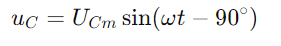 , indicant un canvi de fase de -90 ° (o 90 graus per davant del corrent).El triangle dret del diagrama de fase aclareix això
, indicant un canvi de fase de -90 ° (o 90 graus per davant del corrent).El triangle dret del diagrama de fase aclareix això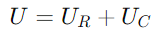 no només està en magnitud, sinó també en relació de fase, amb el vector de tensió del terminal (U) completar el triangle.
no només està en magnitud, sinó també en relació de fase, amb el vector de tensió del terminal (U) completar el triangle.
Figura 13: Diagrama de fase de tensió del circuit de la sèrie RC
Punts clau en l’anàlisi de la sèrie Circuits RC
Impedància en el circuit de la sèrie RC, representat com a Z, combina la resistència (R) i l'efecte reactiu de la capacitança en una sola mesura que varia amb la freqüència del senyal.S’expressa matemàticament com 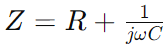 , on ω és la freqüència angular i C és la capacitança.Aquí, R constitueix la part real de la impedància i
, on ω és la freqüència angular i C és la capacitança.Aquí, R constitueix la part real de la impedància i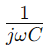 Representa la part imaginària, cosa que indica com el condensador influeix en el circuit.
Representa la part imaginària, cosa que indica com el condensador influeix en el circuit.
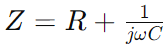 , on ω és la freqüència angular i C és la capacitança.Aquí, R constitueix la part real de la impedància i
, on ω és la freqüència angular i C és la capacitança.Aquí, R constitueix la part real de la impedància i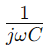 Representa la part imaginària, cosa que indica com el condensador influeix en el circuit.
Representa la part imaginària, cosa que indica com el condensador influeix en el circuit.La manera en què la impedància canvia amb la freqüència és fonamental per utilitzar circuits de sèries RC en aplicacions de filtració.A freqüències inferiors, el circuit presenta una impedància més elevada, bloquejant eficaçment aquestes freqüències.Per contra, a freqüències més altes, la impedància baixa, permetent que aquestes freqüències passin més lliurement.Aquest comportament fa que els circuits de sèries RC siguin ideals per a tasques com filtrar soroll no desitjat de baixa freqüència o passar senyals d’alta freqüència.

Figura 14: Diagrama vectorial d’impedància del circuit de la sèrie RC
Conclusió
Des del filtratge de freqüències no desitjades fins a la conformació de les respostes del senyal, el circuit de la sèrie RC és fonamental en una àmplia gamma de funcions electròniques.En comprendre els principis subjacents com la impedància, les relacions de fase i el comportament dependent de la freqüència d’aquests circuits, enginyers i dissenyadors estan equipats per a solucions artesanes que gestionen eficaçment la integritat del senyal en sistemes electrònics complexos.L’examen detallat d’aquests circuits, recolzat en anàlisis matemàtiques i representacions visuals com els esquemes de fase, ofereix una visió completa que és important per a qualsevol persona que vulgui aprofundir en la comprensió de la dinàmica de circuits electrònics o per millorar les seves habilitats pràctiques en el disseny de circuits i la resolució de problemes.
Preguntes més freqüents [FAQ]
1. Quin és el principi del circuit RC?
El principi d’un circuit RC (resistència-capacitor) gira al voltant dels processos de càrrega i descàrrega del condensador a través de la resistència.En aquest circuit, la capacitat del condensador d’emmagatzemar i alliberar l’energia elèctrica interacciona amb la resistència, que controla la velocitat a la qual el condensador carrega o es descarrega.
2. Per què un circuit RC condueix el corrent?
En un circuit RC, el corrent condueix la tensió a través del condensador perquè el condensador ha de començar a carregar -se abans que la seva tensió pugui augmentar.Atès que el corrent flueix cap al condensador per carregar -lo, el corrent pic abans que la tensió a través del condensador arribi al màxim.Aquest efecte provoca un canvi de fase on la fase de corrent condueix la fase de tensió fins a 90 graus, depenent de la freqüència del senyal d’entrada.
3. Com canvia la tensió en un circuit RC?
El canvi de tensió en un circuit RC durant la càrrega es descriu mitjançant una funció exponencial.Quan s’aplica una tensió, la tensió a través del condensador augmenta inicialment ràpidament, i després s’acosta a mesura que s’acosta a la tensió d’alimentació.Matemàticament, això s'expressa com 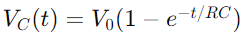 , on VC(t) és la tensió a través del condensador en el moment T, V0 és la tensió de subministrament i RC és la constant de temps del circuit, determinant la rapidesa amb què es carrega el condensador.Per contra, durant la descàrrega, la tensió a través del condensador disminueix exponencialment, seguint l'equació
, on VC(t) és la tensió a través del condensador en el moment T, V0 és la tensió de subministrament i RC és la constant de temps del circuit, determinant la rapidesa amb què es carrega el condensador.Per contra, durant la descàrrega, la tensió a través del condensador disminueix exponencialment, seguint l'equació 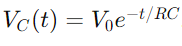 .
.
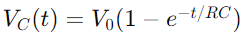 , on VC(t) és la tensió a través del condensador en el moment T, V0 és la tensió de subministrament i RC és la constant de temps del circuit, determinant la rapidesa amb què es carrega el condensador.Per contra, durant la descàrrega, la tensió a través del condensador disminueix exponencialment, seguint l'equació
, on VC(t) és la tensió a través del condensador en el moment T, V0 és la tensió de subministrament i RC és la constant de temps del circuit, determinant la rapidesa amb què es carrega el condensador.Per contra, durant la descàrrega, la tensió a través del condensador disminueix exponencialment, seguint l'equació 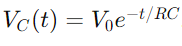 .
. SOBRE NOSALTRES
Satisfacció del client cada vegada.Confiança mútua i interessos comuns.
SOBRE NOSALTRES
Satisfacció del client cada vegada.Confiança mútua i interessos comuns.
Prova de funció.Els productes més rendibles i el millor servei són el nostre compromís etern.
Article calent
- Són intercanviables CR2032 i CR2016
- MOSFET: definició, principi de treball i selecció
- Instal·lació i proves de relé, Interpretació de diagrames de cablejat de relé
- CR2016 vs. CR2032 Quina és la diferència
- NPN vs. PNP: Quina diferència hi ha?
- ESP32 vs STM32: quin microcontrolador és millor per a vosaltres?
- LM358 Amplificador operatiu Dual Guia completa: pinyes, esquemes de circuit, equivalents, exemples útils
- Guia de comparació CR2032 vs DL2032 vs CR2025
- Comprendre les diferències ESP32 i ESP32-S3 Anàlisi tècnica i de rendiment
- Anàlisi detallada del circuit de la sèrie RC
 Anàlisi en profunditat de díodes 1N4148: modes de funcionament, especificacions i escenaris d'ús
Anàlisi en profunditat de díodes 1N4148: modes de funcionament, especificacions i escenaris d'ús
2024-05-08
 Comprensió dels tipus i usos de bombes de desplaçament dinàmiques i positives
Comprensió dels tipus i usos de bombes de desplaçament dinàmiques i positives
2024-05-07
Número de part calenta
 UPS1H010MDD1TA
UPS1H010MDD1TA 06031C681JAT2A
06031C681JAT2A GRM1885C1H7R2CA01D
GRM1885C1H7R2CA01D EMK212BJ105KG-T
EMK212BJ105KG-T 08051A2R4DAT2A
08051A2R4DAT2A GCM3195C1H222JA16D
GCM3195C1H222JA16D CC1206JKNPODBN150
CC1206JKNPODBN150 GRM1555C1E8R0CZ01D
GRM1555C1E8R0CZ01D GRM1555C1H100FZ01D
GRM1555C1H100FZ01D T491B106K025AH
T491B106K025AH
- 1803617
- MK52DN512CLQ10
- MAX98090AETL+T
- JS28F160C3BD70A
- MIC2562A-0YM
- PAM8603ENHR
- RT0402BRE0724K9L
- RT0603BRE07332RL
- RT0402BRE07137KL
- SN74LS32NSR
- LT8471IFE#PBF
- ADM3232EARNZ-REEL7
- AM26LV31CD
- LTC1696ES6#TRMPBF
- LM2577SX-ADJ/NOPB
- LT8301HS5#TRPBF
- T322D226M015AT
- DRV5053VAQDBZRQ1
- MIC2774N-29YM5
- BA6898FP
- BA7762FS
- CAT28F001N-12T
- CBTL06DP211EE
- GAL16LV8C-10LJ
- ICE2QR2280G
- M21050G-14
- M30622MCA-5W9FD
- MC33363BDW
- RPCS5331C.B3-998920
- S71WS128JC0BAWAA
- S82352DT
- TME12B800
- APW7062A
- SG8002JF 107.9
- SAK-TC1782F-320F180HL BA
- TG110-S055N2LF
- UCC14240QDWNRQ1
- KSZ8567STXV-VAO
- MDR-40-2440W